Clinical Trial
Evaluating the Effectiveness of Asthma Treatments Over Time: A Comparative Analysis Using Repeated Measure Models and Multilevel models of Longitudinal Data
1The University of Texas Rio Grande Valley, United States.
2Ball State University, United States. 3University of mines and Technology, Ghana.
*Corresponding Author: Lawrence Mensah Agbota, The University of Texas Rio Grande Valley, United States.
Citation: Agbota L., Nsiah A., Abubakari S. (2024). Evaluating the Effectiveness of Asthma Treatments Over Time: A Comparative Analysis Using Repeated Measure Models and Multilevel models of Longitudinal Data. Clinical Case Reports and Studies, BioRes Scientia Publishers. 7(2):1-13. DOI: 10.59657/2837-2565.brs.24.179
Copyright: © 2024 Lawrence Agbota, this is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Received: August 21, 2024 | Accepted: September 20, 2024 | Published: October 07, 2024
Abstract
Aim: To assess the long-term effectiveness of asthma treatments by comparing the utility of repeated measure models (RMM) and multilevel models (MLM) in analyzing longitudinal data of pulmonary function measured by forced expiratory volume in one second (FEV1), over an extended period.
Subject and Methods: Seventy-two asthma patients were randomized into three groups: standard drug (a), test drug (c), and placebo (p), with 24 patients each. Forced expiratory volume (FEV1) was measured hourly for 8 hours post-treatment, plus a baseline measurement. Repeated measure models (RMM) and Multilevel models (MLM) were used to analyze forced expiratory volume (FEV1) changes over time.
Results: The repeated measures model with an unstructured covariance matrix proved most effective, as indicated by Akaike Information Criterion (AIC) of 342.45, Bayesian Information Criterion (BIC) of 445, and corrected AIC (AICC) of 349.7. This model displayed a correlation decrease in forced expiratory volume (FEV1) from 0.7124 to 0.6429 over 8 hours, with a standard error of 0.1448.
Conclusion: The study supports the use of repeated measures models with an unstructured covariance matrix for analyzing the efficacy of asthma treatments over time. This model effectively captured the dynamics of treatment effects on respiratory function, adhering to assumptions such as linearity, homoscedasticity, normality, and absence of significant outliers, thereby providing robust and reliable results.
Keywords: longitudinal data; repeated measure models; multilevel models; unconditional mean; unconditional growth model; conditional growth
Introduction
The field of medical statistics plays a pivotal role in analyzing clinical trial data, offering insights into the effectiveness of medical treatments. This report is based on a dataset provided by (Littell et al., 2002 and Littell et al., 2006) focusing on a study evaluating the effects of two different drugs on the respiratory function of asthma patients. The primary measure of interest is the forced expiratory volume (FEV) in 1 hour, a critical indicator of pulmonary function. This involves a series of statistical methods, including the plotting of forced expiratory volume (FEV1) profiles over time, fitting mixed models using Statistical Analysis System procedure also known as SAS.
Literature Review
Modeling a longitudinal data on health outcomes in multilevel research settings are very challenging. The challenges are how to deal with changes in measurement over time, how to investigate temporal measurement invariance, how to model residual dependence due to the nested nature of longitudinal data, and how to find the unique correlation over time (Colin et al., 2022). However multilevel modelling is appropriate for analysis of data with a nested structure for example, patient (Level 1) nested within drugs (Level 2). This means ignoring such data can result in biased estimates of standard errors and subsequent increase in Type 1 error (Kessels et al., 2019). Longitudinal data, comprising repeated measurements of the same individuals over time, arise frequently in cardiology and the biomedical sciences in general (Fitzmaurice, 2008). For example, patient and forced expiratory volume (FEV) measurement used repeated measurements of the respiratory ability of patients responding drugs to study changes in respiratory ability over an 8-hour study period.
In many research fields like education and clinical studies, data often have a hierarchical structure. For instance, in education, students are grouped within specific classrooms or under certain teachers, and these teachers are then part of larger school units. Similarly, in social services, individuals receiving services are grouped under particular social workers, who themselves are part of broader local civil service organizations (Huang, 2018). Conducting research at any of these levels while ignoring the more detailed levels (students) or contextual levels (schools) can lead to erroneous conclusions. As such, multilevel models have been developed to properly account for the hierarchical (correlated) nesting of data (McCoach, 2010).
Multilevel modeling (MLM) is a key analytical technique in educational research, especially when data is collected from students within various classrooms or schools, or from the same students at multiple points over time. This approach is crucial to avoid Type-1 errors, which are incorrect positive findings in statistical analysis. MLM provides a more accurate way to handle the complexities of such data structures (Heck and Thomas, 2020). These models are also tailored for data with hierarchical or clustered structures, commonly found across various research fields. For example, in educational research, this includes students within schools, in family studies, children within families, in medical research, patients within medical practices or hospitals, and in biological studies like analyzing dental issues with teeth grouped by different mouths. Such clustering can also stem from research designs, like multistage sampling in large-scale surveys for cost efficiency, resulting in stratified data, or in longitudinal studies where repeated measurements are viewed as nested within individual subjects.
Repeated measures involve observing the same individuals’ multiple times under experimental or observational settings. The key characteristic of repeated measures data is that the measurements are not independent but are correlated because they come from the same subjects. This correlation must be accounted for in any statistical analysis to avoid biased or incorrect conclusions (Lindsey, 1999).
The aim of this report is to apply repeated measure models and multilevel models on longitudinal dataset to understand the effectiveness of drugs on respiratory ability in asthma patients, and to evaluate and compare the strengths and weaknesses of each model by selecting the best model for the dataset.
Data and Methods
The dataset was provided in CSV file format and were collected by a pharmaceutical company which were analyse by (Littell et al., 2002 and Littell et al., 2006). We apply both multilevel model and repeated measure model on an extension from what was analyzed earlier.
The methods used for the report, which entails the various procedures involved in multilevel models and repeated measure model for the longitudinal dataset below are the definition and their equations.
Multilevel Models
Unconditional Mean Model
The Unconditional Mean Model, often referred to as the Null Model or Intercept-only Model, in the context of multilevel linear regression (mixed-effects models), is the simplest form of such a model (Wang et al., 2008). It includes only the intercept in the model without any predictors (fixed or random except for the random intercept). Using the proc mixed to fit the dataset with subject patients nested in drug and class of time, patients and drug. We look at the unconditional mean model.
The unconditional mean model can be mathematically expressed as:
 (1)
(1)


i=index for FEV Measurement
j=index for Patient and
γ_00=over mean measurement for FEV
Unconditional Growth Model
The Unconditional Growth Model is a type of multilevel model used to analyze change over time without including any predictors other than time itself (You and Sharkey, 2009). This model is used to assess how an outcome variable changes over time across different individuals or units. It is "unconditional" because it does not condition on any other covariates except for the time variable.
The Unconditional Growth Model can be represented as follows:
 (2)
(2)


 (3)
(3)
Where, 

Conditional Growth Model
A Conditional Growth Model is also a multilevel modeling. It is an extension of the Unconditional Growth Model (Kuljamin et al., 2011). While the Unconditional Growth Model includes only time as a predictor to assess change over time, the Conditional Growth Model adds additional covariates or predictors to explain more of the variance in the outcome, both within individual patient (Level 1) and between individual patients (Level 2). We introduce the drug, and drug-time interaction in the model.
The conditional Growth Model can be represented as follows:



 (4)
(4)
Also,


Repeated Measure Model
Repeated measure models are particularly useful for studying correlation between measurements taken from the same individual over time. The general form that can be used when analyzing data like the effectiveness of asthma treatments over time is mathematically expressed as:

Where  is the outcome measure for patient
is the outcome measure for patient  at time
at time ,
,  and
and  represent the effects of drug, time, and their interaction, respectively? And
represent the effects of drug, time, and their interaction, respectively? And  is the random effect accounting for individual differences.
is the random effect accounting for individual differences.
To select the best covariance structure, we consider Compound Symmetry (CS) with constant variance and equal correlation, Autoregressive (AR (1)) with decreasing correlation over time, Unstructured (UN) allowing different variances and covariance and the simple model (Wolfinger, 1993). We also look at fitting the models using each structure and compare using criteria like AIC or BIC, choosing the one with the lowest value for a balance between fit and simplicity. Also looking at the trend of the correlation over time. Proc mixed was used to fit the data with class containing patients, drugs and time. The model employed repeated as keyword to repeat the measure over time period with the subject patients nested in drug (Patient (Drug)).
Criteria for Selecting (AIC and BIC)
An examination and comparison of the Bayesian Information Criterion (BIC) and Akaike’s Information Criterion (AIC), two prevalent penalized model selection criteria are important in regression model to determine model fit. There are foundational differences and approaches of AIC and BIC to approximating distinct statistical measures. Similarities in the interpretation of their penalty terms are also very crucial. Their efficacy in selecting appropriate models is analyzed through simulated and real data sets on social mobility. The use of both AIC and BIC in longitudinal dataset is advocated for more informed model selection, particularly in identifying models that satisfy both criteria (Vrieze, 2012). Mathematically, AIC and BIC is express as



Where LL represent the Log Likelihood and p represent the number of parameters.
Results and Discussion
Result
Proc sgpanel was used to fit the data paneled by Drugs (standard drug a, test drug c, and placebo p) and also group by patients nested with the drug. Below is the individual profile.
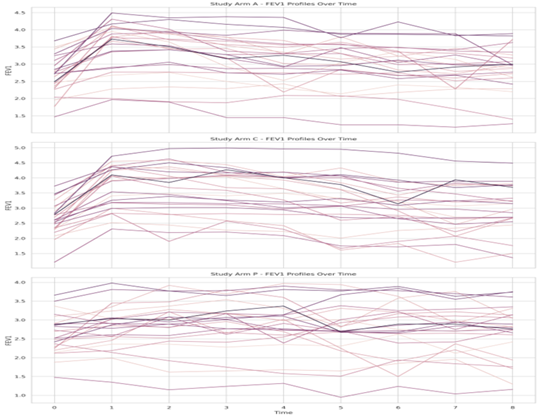
Figure 1: Individual FEV1 profile
From Figure 1, we examine the efficacy of three drugs on FEV1 levels over time. This figure contains 72 patients randomized with 24 patients in each of the three study arms. These drugs were administered to each patient and a standard measure of respiratory ability called FEV1 was measured in one hour over 8 hours following the treatment which is a critical measure of lung function, with higher values indicating better respiratory capacity. The drugs are labeled as (a) the standard drug, (c) the test drug, and (p) the placebo. The standard drug (a) shows a significant increase in FEV1 levels, peaking around the midpoint of the time scale. This suggests that drug (a) has a substantial, yet temporary, effect on lung function, likely due to its pharmacodynamics properties. After reaching the peak, the FEV1 levels decline, which could be due to the drug's effects wearing off or the body's natural progression of the underlying condition. The test drug (c) demonstrates a more pronounced effect on FEV1, with an even higher peak than the standard drug (a). This indicates that drug (c) may have a stronger or more sustained action on the lungs. However, similar to the standard drug, the FEV1 levels eventually return towards baseline, reflecting the transient nature of the drug's efficacy or potential adaptive responses by the patients’ physiology.
In contrast, the placebo (p) exhibits no significant change in FEV1 levels over time. The lack of improvement suggests that the placebo does not have a therapeutic effect on lung function. The flat trend line for the placebo serves as a control, indicating that the increases observed with drugs (a) and (c) are likely due to their active ingredients rather than psychological or spontaneous physiological changes. The individual patient lines within each drug category reveal variations in response to treatment. This heterogeneity underscores the complexity of treating respiratory conditions and the need for personalized medicine approaches.
Overall, the graph suggests that while both the standard drug a, and test drugs c, can improve lung function, their effects are not long-lasting, and there is considerable variability in patient response. Further analysis would be required to understand the duration of the drugs' action and the implications for treatment regimens, such as the potential need for multiple dosing to maintain improved lung function.
Also, proc sql was used to create the dataset which calculated the mean of FEV grouped by Tine and Drug. We then employed proc sqplot to allow the mean dataset created using sql to be plotted for each drug since each patient are nested within drugs. Below is the graph.
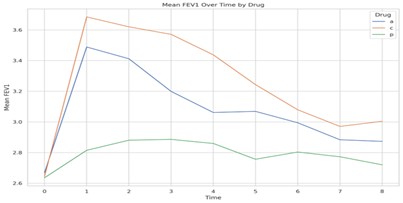
Figure 2: Mean FEV1 plot
The individual FEV1 profile plot in (Figure 1) and the mean FEV1 plot in (Figure 2) serve different analytical purposes. In Figure 1, individual patient data is plotted, which allows for the observation of each patient's reaction to the treatments over time, revealing the range of responses and potential outliers. This detail is crucial for understanding individual variations in drug efficacy and for identifying any adverse responses that may not be apparent in group averages. Conversely, Figure 2 provides a summarized view by displaying the mean FEV1 values at each time point for the groups treated with drugs (a), (c), and placebo (p). At time = 0, the mean FEV1 levels for all treatments are identical, establishing a uniform baseline from which the efficacy of the drugs can be compared. This is crucial because it demonstrates that any subsequent changes are due to the drugs' effects rather than initial differences in lung function.
At time = 1, the plot reveals that the test drug (c) induces a significant elevation in mean FEV1, surpassing the standard drug (a) and greatly outperforming the placebo (p). This suggests that drug (c) is the most effective at improving lung function within the first hour. The standard drug (a) also increases mean FEV1, but to a lesser degree, while the placebo (p) shows only a marginal increase, which could be attributed to a placebo effect or natural physiological variation. The mean FEV1 plot, with its focus on average responses, offers a more streamlined and arguably clearer comparison of the drugs' efficacy over time. However, it obscures the individual variability presented in Figure 1. Both plots together provide a comprehensive understanding of the drugs' performance, highlighting both the average effectiveness and the range of individual patient responses. In conclusion the individual plot of FEV 1 in figure 1, talks about observation of each patient’s reaction to treatments over time while the mean FEV 1 provides a summarized view by displaying the mean FEV1 values at each time point for the groups treated with drugs (a), (c), and placebo (p) respectively.
Repeated Measure Mixed Model
We consider the covariance and correlation estimates for FEV1 repeated measure for the unstructured and structured model. We also look at their various AIC AICC, BIC and -2Res Log Likelihood together with their F-test values. Below are the tables.
Table 1: REML Covariance and Correlation estimates for FEV1 repeated measure data Unstructured
| Time 0 | Time 1 | Time 2 | Time 3 | Time 4 | Time 5 | Time 6 | Time 7 | Time 8 |
| 0.291 | 0.259 | 0.2748 | 0.2649 | 0.2412 | 0.294 | 0.2619 | 0.2597 | 0.246 |
| 0.7124 | 0.4541 | 0.4587 | 0.4441 | 0.4154 | 0.4349 | 0.3934 | 0.3562 | 0.384 |
| 0.7091 | 0.9474 | 0.5163 | 0.4808 | 0.4688 | 0.4943 | 0.4254 | 0.3992 | 0.4257 |
| 0.6999 | 0.9393 | 0.9536 | 0.4923 | 0.4687 | 0.4843 | 0.4263 | 0.4021 | 0.4256 |
| 0.6363 | 0.8773 | 0.9284 | 0.9506 | 0.4938 | 0.4837 | 0.4179 | 0.4023 | 0.4251 |
| 0.717 | 0.849 | 0.905 | 0.908 | 0.9055 | 0.5779 | 0.4945 | 0.4643 | 0.495 |
| 0.6932 | 0.8334 | 0.8453 | 0.8674 | 0.849 | 0.9286 | 0.4906 | 0.4454 | 0.4632 |
| 0.6813 | 0.7479 | 0.7861 | 0.8109 | 0.8102 | 0.8642 | 0.8997 | 0.4994 | 0.4496 |
| 0.6429 | 0.8033 | 0.8352 | 0.8552 | 0.8529 | 0.9181 | 0.9323 | 0.897 | 0.5031 |
Variances on the diagonal, covariance above diagonal, correlations between diagonal.
Table 2: REML variance, covariance and correlation estimates for five covariance covariance structures for FEV1 repeated measures.
| Time 0 | Time 1 | Time 2 | Time 3 | Time 4 | Time 5 | Time 6 | Time 7 | Time 8 |
| Simple | ||||||||
| 0.4798 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| CS | ||||||||
| 0.4798 | 0.4008 | 0.4008 | 0.4008 | 0.4008 | 0.4008 | 0.4008 | 0.4008 | 0.4008 |
| 1 | 0.8354 | 0.8354 | 0.8354 | 0.8354 | 0.8354 | 0.8354 | 0.8354 | 0.8354 |
| Toeplitz | ||||||||
| 0.4357 | 0.3879 | 0.3696 | 0.3555 | 0.3328 | 0.3244 | 0.3134 | 0.3092 | 0.2877 |
| 1 | 0.8904 | 0.8482 | 0.8159 | 0.7639 | 0.7446 | 0.7194 | 0.7096 | 0.6602 |
| AR(1) | ||||||||
| 0.4413 | 0.3939 | 0.3517 | 0.3139 | 0.2803 | 0.2502 | 0.2234 | 0.1994 | 0.178 |
| 1 | 0.8927 | 0.797 | 0.7115 | 0.6351 | 0.567 | 0.5062 | 0.4519 | 0.4034 |
Variances and covariance in top line correlations in bottom line.
Table 3: REML Akaike’s information criterion (AIC) and Schwarz’s Bayesian criterion (SBC) for five covariance structures
| AIC | AICC | BIC | -2RLL | |
| Simple | 1394.1 | 1394.1 | 1396.4 | 1392.1 |
| Cs | 540.9 | 541 | 545.5 | 536 |
| Toeplitz | 430.5 | 430.8 | 451 | 412.5 |
| UN | 342.5 | 349.7 | 445 | 252.5 |
| Ar(1) | 464 | 464 | 468.5 | 460.0 |
Table 4: REML Values of F test for fixed effects for the five covariance structures
| Structure Name | Time | Drug | Drug*Time |
| Simple | 7.67 | 24.02 | 1.18 |
| Compound Symmetry | 46.58 | 3.13 | 7.14 |
| AR (1) | 46.16 | 3.95 | 7.60 |
| Toeplitz | 54.62 | 3.55 | 8.42 |
| UN | 25.12 | 3.13 | 5.24 |
Table 5: REML Model Selected output (UN Model)
| Effect | DRUG | time | Estimate | Stand. Error | DF | t Value | Pr > |t| |
| Intercept | 2.7204 | 0.1448 | 69 | 18.79 | <.0001 | ||
| DRUG | a | 0.1529 | 0.2048 | 69 | 0.75 | 0.4577 | |
| DRUG | c | 0.2837 | 0.2048 | 69 | 1.39 | 0.1703 | |
| DRUG | p | 0 | . | . | . | . | |
| time | 0 | -0.0846 | 0.1122 | 69 | -0.75 | 0.4535 | |
| time | 1 | 0.09458 | 0.0888 | 69 | 1.07 | 0.2906 | |
| time | 2 | 0.1604 | 0.08368 | 69 | 1.92 | 0.0594 | |
| time | 3 | 0.1658 | 0.0775 | 69 | 2.14 | 0.0359 | |
| time | 4 | 0.1392 | 0.07818 | 69 | 1.78 | 0.0795 | |
| time | 5 | 0.03625 | 0.06156 | 69 | 0.59 | 0.5579 | |
| time | 6 | 0.08333 | 0.05297 | 69 | 1.57 | 0.1203 | |
| time | 7 | 0.0525 | 0.0656 | 69 | 0.8 | 0.4263 | |
| time | 8 | 0 | . | . | . | . | |
| DRUG*time | a | 0 | -0.1204 | 0.1587 | 69 | -0.76 | 0.4505 |
| DRUG*time | a | 1 | 0.5208 | 0.1256 | 69 | 4.15 | <.0001 |
| DRUG*time | a | 2 | 0.3783 | 0.1183 | 69 | 3.2 | 0.0021 |
| DRUG*time | a | 3 | 0.16 | 0.1096 | 69 | 1.46 | 0.1489 |
| DRUG*time | a | 4 | 0.04917 | 0.1106 | 69 | 0.44 | 0.6579 |
| DRUG*time | a | 5 | 0.1592 | 0.08706 | 69 | 1.83 | 0.0718 |
| DRUG*time | a | 6 | 0.03792 | 0.07492 | 69 | 0.51 | 0.6144 |
| DRUG*time | a | 7 | -0.0421 | 0.09277 | 69 | -0.45 | 0.6515 |
| DRUG*time | a | 8 | 0 | . | . | . | . |
| DRUG*time | c | 0 | -0.2758 | 0.1587 | 69 | -1.74 | 0.0866 |
| DRUG*time | c | 1 | 0.5863 | 0.1256 | 69 | 4.67 | <.0001 |
| DRUG*time | c | 2 | 0.4558 | 0.1183 | 69 | 3.85 | 0.0003 |
| DRUG*time | c | 3 | 0.4013 | 0.1096 | 69 | 3.66 | 0.0005 |
| DRUG*time | c | 4 | 0.2942 | 0.1106 | 69 | 2.66 | 0.0097 |
| DRUG*time | c | 5 | 0.2029 | 0.08706 | 69 | 2.33 | 0.0227 |
| DRUG*time | c | 6 | -0.0083 | 0.07492 | 69 | -0.11 | 0.9118 |
| DRUG*time | c | 7 | -0.0858 | 0.09277 | 69 | -0.93 | 0.3581 |
| DRUG*time | c | 8 | 0 | . | . | . | . |
Multilevel model
We estimate the covariance parameters of the UN model for all the multilevel models.
Table 6: REML Covariance Parameter for Unconditional Mean Model
| Covariance Parameter Estimates | |||||
| Cov Parm. | Subject | Estimate | Standard | Z Val. | Pr > Z |
| Error | |||||
| UN (1,1) | PATIENT(DRUG) | 0.4183 | 0.07287 | 5.74 | <.0001 |
| Residual | 0.1425 | 0.0084 | 16.97 | <.0001 | |
Table 7: REML Solution for Fixed Effect
| Effect | Estimate | Standard | DF | t Value | Pr > |t| | Alpha | Lower | Upper |
| Error | ||||||||
| Intercept | 3.0384 | 0.07765 | 71 | 39.13 | <.0001 | 0.05 | 2.8836 | 3.1932 |
Table 8: REML Covariance Parameter for Unconditional Growth Model
| Cov Parm | Subject | Estimate | Standard Error | Z Value | Pr Z |
| UN (1,1) | PATIENT(DRUG) | 0.379 | 0.07179 | 5.28 | <.0001 |
| UN (2,1) | PATIENT(DRUG) | 0.002199 | 0.00474 | 0.46 | 0.6427 |
| UN (2,2) | PATIENT(DRUG) | 0.001458 | 0.000617 | 2.36 | 0.0091 |
| Residual | 0.1279 | 0.008059 | 15.87 | <.0001 |
Table 9: REML Solution for Fixed Effect
| Effect | Estimate | Standard Error | DF | t Value | Pr > |t| |
| Intercept | 3.1305 | 0.07704 | 71 | 40.63 | <.0001 |
| time | -0.02302 | 0.00706 | 575 | -3.26 | 0.0012 |
Table 10: REML Covariance Parameter for Conditional Growth Model
| Cov Parm | Subject | Estimate | Standard Error | Z Value | Pr Z |
| UN (1,1) | PATIENT(DRUG) | 0.3273 | 0.06402 | 5.11 | <.0001 |
| UN (2,1) | PATIENT(DRUG) | 0.005893 | 0.00438 | 1.35 | 0.178 |
| UN (2,2) | PATIENT(DRUG) | 0.001313 | 0.0006 | 2.18 | 0.0146 |
| Residual | 0.1279 | 0.00806 | 15.87 | <.0001 |
Table 11: REML Solution for Fixed Effect
| Effect | DRUG | Estimate | Standard | DF | t Value | Pr > |t| |
| Error | ||||||
| Intercept | 2.7971 | 0.1251 | 69 | 22.36 | <.0001 | |
| DRUG | a | 0.4058 | 0.1769 | 69 | 2.29 | 0.0248 |
| DRUG | c | 0.5942 | 0.1769 | 69 | 3.36 | 0.0013 |
| DRUG | p | 0 | . | . | . | . |
| time | -0.00119 | 0.01198 | 573 | -0.1 | 0.9206 | |
| time*DRUG | a | -0.03148 | 0.01694 | 573 | -1.86 | 0.0637 |
| time*DRUG | c | -0.03399 | 0.01694 | 573 | -2.01 | 0.0453 |
| time*DRUG | p | 0 | . | . | . | . |
Interaction Effects
Table 12: New Estimate for the interaction at Drug a and c
| Label | Estimate | Standard Error | DF | t Value | Pr > |t| |
| time at Drug = a | -0.0327 | 0.01198 | 573 | -2.73 | 0.0066 |
| time at Drug = c | -0.0352 | 0.01198 | 573 | -2.94 | 0.0034 |
| time at Drug = p | -0.0012 | 0.01198 | 573 | -0.1 | 0.9206 |
Table 13: Comparison of the two models fitted for both Repeated and Multilevel
| Procedure | Model Selected | AIC | AICC | BIC | -2RL | Intercept Estimate | Standard Error |
| Repeated Measures | Unstructured | 342.5 | 349.7 | 445 | 252.5 | 2.7204 | 0.1448 |
| Multilevel Coefficient | Conditional Growth model | 806.4 | 806.5 | 815.5 | 798.4 | 2.7971 | 0.1251 |
Discussion
Covariance and correlations are presented above and below the diagonal, respectively, of the matrix in (Table 1). The correlations between FEV1 at Time = 0 and later times are in the first column of the matrix. Correlations generally decrease from 0.7124 between FEV1 at Time = 0 and Time = 1 down to 0.6429 between FEV1 at Time = 0 and Time = 8. Similar decreases are found between FEV1 at Time = 1 and later times, between FEV1 at Time = 2 and later times and so on. This decrease in correlation shows a trend in the repeated measure for a specific time period. The values of the correlations indicate that across the time interval the measurement of FEV 1 is unique across the time interval over the 8 hours. In summary, correlations between pairs of FEV1 measurements decrease with the number of hours between the times at which the measurements were obtained. This is a common phenomenon with repeated measures data. Moreover, magnitudes of correlations between FEV1 repeated measures are similar for pairs of hours with the same interval between hours. Next, we look at the five models to check their trends in the correlation patterns in a table 2.
The table above (Table 2) is a structured covariances which comprises of structured models namely Simple model, Compound Symmetry, Toeplitz and First order Autoregressive. The table is arranged in variance estimate at the top line and correlation estimate at the bottom line. We see that no correlation is assumed in simple model between repeated measures and the variance remains constant (0.4798) over the time interval. This is a very restrictive model and rarely used in practice for repeated measures because it does not account for within-subject correlations. Also, for Compound Symmetry, it assumes that every pair of repeated measures over time has the same correlation (0.8354), regardless of the time interval between them, and the variances are constant over time (0.4008). Also, Toeplitz assume that the correlation between two time points depends only on the time lag between them and not the specific times involved. The correlations decrease as the time lag increases (from 0.8904 to 0.6602), which suggest that the influence of an observation diminishes as more time passes. The variances are not constant, varying from 0.4357 to 0.2877, which indicates changing variability over time period. We again, see that AR (1) correlation estimates and Toeplitz correlation estimates shows a trend of decrease of correlation with length of time interval. This assumes that the correlation between two time points decreases exponentially with the time lag, reflecting that only the previous time point has a significant influence on the current measurement. This is reflected in the pattern where correlations decrease more rapidly as the lag increases (from 0.8927 to 0.4034). The variances, like in the Toeplitz structure, are not constant and decrease over time (from 0.4413 to 0.178).
Looking at the table 3 containing the AIC, AICC, and BIC values for the various models, with conclusions about how well each model fits the data by selecting the model with the lowest AIC. In simple model, we see that it contains the highest AIC and BIC values (1394.1 and 1396.4, respectively), this model is the least effective at describing the data. It is too simplistic because it assumes there is no correlation between the FEV 1 measurements over the 8 hours, which is not usually the case in repeated measures. Again, the Compound Symmetry model shows much better AIC and BIC values (540.9 and 545.5) than the Simple model, which means it fits the data better. However, it still assumes that all time intervals are equally correlated, which does not typically happen in real-world data. Also, the Toeplitz model gives lower AIC and BIC values (430.5 and 451) compared to the CS model, indicating a better fit. This model assumes that FEV1 measurements closer in time are more related than those further apart. This is a more realistic approach and is less complex than the unstructured model. Again, the Unstructured model has the lowest AIC and BIC values (342.5 and 445), suggesting it fits the data the best and it treats each measurement as having a unique relationship with every other one over time intervals. Finally in the AR (1) model, AIC and BIC values (464 and 468.5) are higher than those for the Toeplitz and unstructured models but still lower than those for the Simple and CS models. It is a model that assumes that each measurement is mainly related to the one right before it, which simplifies things but might miss some nuances. We also look at the corresponding F-test values of the fixed solution for each of the models.
From table 4, F values for tests of Time and DRUG ∗ Time interaction in the simple structure model are excessively small due to the fact that Simple model underestimates covariance between observations far apart in time, and thereby overestimates variances of divergences between these observations. Results of F tests based on CS and AR (1) covariance are similar for fixed effects. These structures are adequate for modelling the covariance, and therefore produce valid estimates of error. Also, for Toeplitz and UN, their F test for Drug is similar but that of Time and Drug*Time are different.
In conclusion we select the unstructured model from the repeated measure model because it has the lowest AIC of 342.5 and BIC of 445 values and also treat each measurement of FEV1 as a unique correlation over the time interval. Despite it huge parameters of 45, it explains the within-subjects correlations of the patients nested in drugs in a unique trends over the 8 hours’ time intervals.
From table 5 above, using Drug p as reference point, we see that drug group a and c are not statistically significant with p-values 0.4577 and 0.1703 respectively with their t-values of 0.75 and 1.39 which also yields same standard error of 0.2048. It appears that the only parameter estimates which is significant at that reference point is the intercept with p-value of 0.0001 and standard error of 0.1448 associated with t-value of 18.79. This suggest that when the predictors are zero the mean measurement for FEV (baseline measurement) is 2.7204. It also means that on average, the FEV mean measurement is expected to increase by 2.7204 units when considering the intercept and when all other variables are at zero, which typically serves as a starting point for the model rather than a practical prediction. Again using time = 8, as a reference point, we also noticed that at Time = 0, Time = 1, Time =2, Time =4, Time = 5 , Time = 6 and Time =7 the estimates are not statistically significant with p-value 0.4535, 0.2906, 0.0594, 0.0795, 0.5579, 0.1203 and 0.4263 with the corresponding t-value of -0.75, 1.07, 1.92, 1.78, 0.59, 1.57 and 0.08 which also yields a standard errors of 0.1122, 0.08880, 0.08368 , 0.07818, 0.06156 , 0.05297 and 0.06560.We see that the only time that is statistically significant occurs at Time =3, with p-value of 0.0359 and t-value of 2.14 which also produces a standard error of 0.07750. This means that, on average, an increase of one unit in time is expected to result in a mean change of 0.1658 units in the FEV measurement. Also, using Time = 8 with Drug – Time interactions as reference point, we see that Drug – time interactions of at Time = 0, Time = 3, Time = 4, Time = 5, Time = 6 and Time = 7 estimates are not statistically significant with p-value of 0.4505, 0.1489, 0.6579, 0.0718, 0.6144 and 0.6515 respectively. We also see that, only Drug - time interaction at Drug an at time = 1, time =2 are the only significant estimates with t-values of 4.15 and 3.20 and p-value of 0.0001 and 0.0021 respectively. Also produces a standard error of 0.1256 and 0.1183. This also means that, on average, an increase of one unit in Drug – time interaction is expected to result in a mean change of 0.5208 and 0.3783 units respectively in the FEV measurement.
Again, using Drug - time interaction at Drug c when Time = 8 as reference, we see that drug-time interaction at c when Time = 0, Time = 6, Time = 7 are not statistically significant with p-values of 0.0866, 0.9118 and 0.3581 respectively with t-values of -1.74, -0.11 and -0.93 which also produces standard errors 0.158, 0.07492 and 0.9277 respectively.
It appears that the only estimators that are statistically significant in the drug-time interaction are Time =1, Time = 2, Time = 3, Time = 4 and Time = 5 with p-values 0.0001, 0.0003, 0.0005, 0.0097 and 0.0227 with the corresponding t-value 4.67, 3.85, 3.66, 2.66 and 2.33 with standard errors of 0.1256, 0.1183, 0.1096, 0.1106 and 0.08706. This also means that, on average, an increase of one unit in Drug – time interaction is expected to result in a mean change of 0.5863, 0.4558, 0.4013, 0.2942 and 0.2029 units respectively in the FEV measurement. This means that taking the model that is not significant from the model will not affect the model predictions. In proc mixed, the statement MODEL includes intercept as default. Therefore, we can further request that intercept be random in the random statement. There are different estimation methods that proc mixed can use. The default is residual (restricted) maximum likelihood and is the method that we use here. The option solution in the model statement gives the parameter estimates for the fixed effect. The option covtest requests for the standard error for the covariance-variance parameter estimates and the corresponding z-test. The option noclprint requests that SAS not print the class information.
From Table 6, the estimated between variance,  corresponds to the term intercept (baseline measurement) in the output of the covariance parameters estimates and the estimated with variance,
corresponds to the term intercept (baseline measurement) in the output of the covariance parameters estimates and the estimated with variance,  corresponds to the term Residual in the same output section. From the table we see that the variance between patients nested in a drug in their FEV1 mean measurement,
corresponds to the term Residual in the same output section. From the table we see that the variance between patients nested in a drug in their FEV1 mean measurement,  which yields standard deviation of 0.07287 and it significant at p-value of 0. 0001. Also, we notice that variance within the residuals,
which yields standard deviation of 0.07287 and it significant at p-value of 0. 0001. Also, we notice that variance within the residuals,  which also produces a standard error of 0.008395 which is also significant at p-value =0.0001.
which also produces a standard error of 0.008395 which is also significant at p-value =0.0001.
To measure the magnitude of the variation among patients nested in drug in the mean FEV level we calculating the ICC by:

This tells us about the portion of variation that occurs between patients nested in a drug in their mean FEV measurement levels.
To measure the magnitude of the variation among patients in their mean FEV levels, we can calculate the plausible values range for these means, based on the between variance, we obtained from the model the range of values that lies between the means of the FEV measurement, thus 
 as the interval.
as the interval.
From table 7, the coefficient for the constant is the predicted FEV1 measurement when all predictors are 0, so when the average patients time = 0, the FEV1 (baseline measurement) is predicted to be 3.0384. This means that on average, the FEV mean measurement is expected to increase by 3.0384 units when considering the intercept and when all other variables are at zero, which typically serves as a starting point for the model rather than a practical prediction. This estimate yields a standard error of 0.07765 with p-value of 0.001 and lies between (2.8836, 3.1932).
Now from table 8, we consider the covariance parameter estimates, which tell us how much these intercepts and slopes vary across patients. We may rewrite it as:

From the matrix above, the covariance is
is  with standard error 0.004740 that yields a p-value of 0. 6427.This is saying that there is no evidence that the effect of time depending upon the average forced expiratory volume (FEV) in the patients. The covariance
with standard error 0.004740 that yields a p-value of 0. 6427.This is saying that there is no evidence that the effect of time depending upon the average forced expiratory volume (FEV) in the patients. The covariance  estimate denoted with UN (1,1) correspond to the intercept which is 0.3790 and it is significant at p-value of 0.0001 with standard error of 0.07179.
estimate denoted with UN (1,1) correspond to the intercept which is 0.3790 and it is significant at p-value of 0.0001 with standard error of 0.07179.
The parameter corresponding to UN (2,2) is the variability in slopes of time. The estimate is 0.001458 with standard error 0.000617. Which yields a p-value of 0.0091 for 1-tailed test.
The test being significant tells us that we cannot accept the hypothesis that there is no difference in slope among patients nested in drug.
Noticed that the residual variance is now 0.1279, comparing with the residual variance of 0.1425 in the one-way ANOVA with random effect model. The variance component representing variation between patients decreases greatly (from 0.4183 to 0.379). This means that the time variable explains a small portion of the patient-to-patient variation in mean forced expiratory volume (FEV) measurement. More precisely, the proportion of variance explained by time is
 ,
,
that is about  of the explainable variation in patient mean forced expiratory volume (FEV) measurement is explained by time. The variance within patient (the residual) changes slightly also from 0.1425 in unconditional mean model to 0.1279 in in the unconditional growth model.
of the explainable variation in patient mean forced expiratory volume (FEV) measurement is explained by time. The variance within patient (the residual) changes slightly also from 0.1425 in unconditional mean model to 0.1279 in in the unconditional growth model.
From Table 9, we see that  pausible value range for the patients mean is between,
pausible value range for the patients mean is between,  =
=  . And the
. And the  pausible value range for the Time - Slope mean is
pausible value range for the Time - Slope mean is  =
=  . This means that on average, the forced expiratory volume (FEV) mean measurement is expected to increase by 3.1305 units when considering the intercept and when all other variables are at zero, which typically serves as a starting point for the model rather than a practical prediction with p-value of 0.0001 and yields standard deviation of 0.07704
. This means that on average, the forced expiratory volume (FEV) mean measurement is expected to increase by 3.1305 units when considering the intercept and when all other variables are at zero, which typically serves as a starting point for the model rather than a practical prediction with p-value of 0.0001 and yields standard deviation of 0.07704
Also, on average, an increase of one unit in time is expected to result in a mean decrease of 0.02302 units in the forced expiratory volume (FEV) measurement with p-value of 0.0012 and yields a standard error of 0.00706.
From table 10 we consider the covariance parameter estimates, which tell us how much these intercepts and slopes vary across patients. We may rewrite them again as:

The covariance  estimate denoted with UN (2,1) is 0.005893 with standard error 0.00438 that yields a p-value of 0. 178.This is also saying that there is no evidence that the effect of predictors depending upon the average forced expiratory volume (FEV) in the patients. From table 10 again, we see that, the intercept variance UN (1,1) is significant with p-value < 0>
estimate denoted with UN (2,1) is 0.005893 with standard error 0.00438 that yields a p-value of 0. 178.This is also saying that there is no evidence that the effect of predictors depending upon the average forced expiratory volume (FEV) in the patients. From table 10 again, we see that, the intercept variance UN (1,1) is significant with p-value < 0>
From table 11, using Drug P as a reference, we see that the intercept is significant with p-value of 0.0001 which yields a standard error of 0.1251. This means that on average, the forced expiratory volume (FEV) mean measurement is expected to increase by 2.7971 units when considering the intercept and when all other variables are at zero, which typically serves as a starting point for the model rather than a practical prediction. We also see that Drug a and c are also statistically significant with p-values of 0.0248, 0.0013 which yields same standard error of 0.1769. This also tell us that on average, an increase of one unit in drug group a and c are expected to result in a mean change of 0.0.4058 and 0.5942 units in the forced expiratory volume (FEV) measurement. Again, using Time*Drug interaction at p as reference, we see that time, and drug – time interaction at a are not statistically significant with p-value of 0.9206 and 0.0637 respectively. We also see that only time – drug interaction at c is statistically significant with p-value of 0.0453 which yields a standard error of 0.01694.
This means that on average, an increase in one unit in drug-time interaction is expected to result in a decrease in the mean change by 0.03399 units in the forced expiratory volume (FEV) measurement.
From table 12, we estimate a new drug – time interaction at a specific time. These estimates were added to the proc mixed procedure. This is to validate that though drug-time interaction at the repeated measure analysis is not significant but at a specific time it becomes significant. We see that, at a specific time-drug interaction, thus time at drug = a, the estimate becomes significant with p-value of 0.0066 which yields a standard error of 0.01198 as compared to the previous repeated measure whose p-value was 0.0637 with the corresponding standard error of 0.01694. This means that on average, an increase in one unit in drug-time interaction at specific time is expected to result in a decrease in the mean change by 0.0327 units in the forced expiratory volume (FEV) measurement. We also see that time-drug interaction at c was again significate with p-value = 0.0034 with standard error 0.01198 as compared to the previous in the repeated measure. We see that the standard error produced at this time became very small as compared to the repeated measure. We also see that time-drug interaction at p, is still not significant because it was served as reference point in the repeated measure.
From table 13, we compare the final model and select which model best explains the dataset. Repeated measures (Unstructured) were the model selected because it has AIC of 342.5, AICC of 349.7, BIC of 445 and the -2RLL of 252.5 which is the lowest among the all the models. This suggests that, in terms of the balance between model complexity and goodness of fit, this model is preferable.
Model Assumptions
Linearity and Homoscedasticity
In the analysis, the residual and the studentized residual shows that there is no clear pattern, non-linear shape and no major fan shape which suggests that the linearity and homoscedasticity assumptions are not grossly violated. However, there seems to be a slight fan shape, with the variance of residuals increasing as the predicted mean increases, which could indicate potential heteroscedasticity, however this does not affect the model predictions.
Normality
For normality, both the residual for forced expiratory volume and the studentized residual shows that the residual is approximately normal, looks fairly symmetrical and bell-shaped, which suggest that the model is good. The Q-Q plots from both the residual for forced expiratory volume and the studentized residual however, deviates from the straight line in the tails, especially in the lower tail, suggesting that the residuals may have a slight departure from normality, with potentially heavier tails than the normal distribution would predict but again this does not affect the mode predictions.
Influence and Outliers
It appears that across all plots, there are no systematic patterns in the residuals, which would suggest non-linearity. Although, there are outliers present in all plots, which could potentially influence the model's estimates but these influence does not affect the model for predictions. In conclusion, residuals' distribution suggests that the model assumptions of homoscedasticity and linearity are not grossly violated. However, the presence of outliers indicates that some data points do not fit the model well. These outliers might warrant further investigation to determine if they are influential points or if there's a substantive reason for their divergence from the model's predictions. It would also be important to assess whether these points are due to measurement error, data entry error, or if they represent true variability in the response to treatment.
Conclusion
In conclusion, the analysis of forced expiratory volume (FEV1) measurements across different drug treatments and time points presents distinct methodological considerations. The Unstructured (UN) Repeated Measures model offers detailed insights by allowing unique correlations between each time point, making it ideal for capturing individual variability in response to treatments. Its flexibility is advantageous when the research focus is on the nuanced patterns of change in forced expiratory volume (FEV1), and the dataset is robust enough to support complex modeling without overfitting.
References
- olin-Chevalier, R., Dutheil, F., Cambier, S., Dewavrin, S., Cornet, T., et al. (2022). Methodological issues in analyzing real-world longitudinal occupational health data: A useful guide to approaching the topic. International Journal of Environmental Research and Public Health, 19(12):7023.
Publisher | Google Scholor - Fitzmaurice, G. M., & Ravichandran, C. (2008). A primer in longitudinal data analysis. Circulation, 118(19):2005-2010.
Publisher | Google Scholor - Heck, R., & Thomas, S. L. (2020). An introduction to multilevel modeling techniques: MLM and SEM approaches. Routledge.
Publisher | Google Scholor - Huang, F. L. (2018). Multilevel modeling myths. School Psychology Quarterly, 33(3):492.
Publisher | Google Scholor - Kessels, R., Bloemers, J., Tuiten, A., & van der Heijden, P. G. M. (2019). Multilevel analyses of on-demand medication data, with an application to the treatment of female sexual interest/arousal disorder. PLoS ONE, 14(8):e0221063.
Publisher | Google Scholor - Kuljanin, G., Braun, M. T., & DeShon, R. P. (2011). A cautionary note on modeling growth trends in longitudinal data. Psychological Methods, 16(3):249.
Publisher | Google Scholor - Lindsey, J. K. (1999). Models for repeated measurements. Oxford University Press.
Publisher | Google Scholor - Little, R. J. A., & Rubin, D. B. (2002). Statistical analysis with missing data (2nd ed.). John Wiley & Sons.
Publisher | Google Scholor - Littell, R. C., Milliken, G. A., Stroup, W. W., Wolfinger, R. D., & Schabenberger, O. (2006). SAS for mixed models (2nd ed.). SAS Institute Inc.
Publisher | Google Scholor - McCoach, D. B. (2010). Hierarchical linear modeling. In The reviewer’s guide to quantitative methods in the social sciences, 123-140.
Publisher | Google Scholor - Vrieze, S. I. (2012). Model selection and psychological theory: A discussion of the differences between the Akaike information criterion (AIC) and the Bayesian information criterion (BIC). Psychological Methods, 17(2):228.
Publisher | Google Scholor - Wang, J. C., Xie, H. Y., & Jiang, B. F. (2008). Multilevel models: Applications using SAS. Library of Congress, 495.
Publisher | Google Scholor - Wolfinger, R. (1993). Covariance structure selection in general mixed models. Communications in Statistics - Simulation and Computation, 22(4):1079-1106.
Publisher | Google Scholor - You, S., & Sharkey, J. (2009). Testing a developmental–ecological model of student engagement: A multilevel latent growth curve analysis. Educational Psychology, 29(6):659-684.
Publisher | Google Scholor