A Pure Mathematical Proof of 4-Colour Theorem

This work "A Pure Mathematical Proof of the 4-Colour Theorem" is related to the previous proof assisted by computer. "Triangulations of Euler Convex Polygon" provides a fresh beginning point for the proof. The central concept is to discover an extended invariance property of Standard Graph’s boundary, which is described as "3-Colour All Phase States (3CP)" in this work and it is demonstrated that the Standard Graph’s boundary and sub-bound are 3CP and 4-colorable (4-3CP) via the Expanded Operation e(+, pi) and e(-, pi). It's exciting that this regularity was discovered for the first time and the 4-3CP invariance can naturally derive the 4-Colour Theorem. The majority of the definitions, theorems and proof strategies are shown in this work.

The 4-Colour Theorem states that every map can be colored using only four colors and no two adjacent regions have the same color. The initial problem was first posed in the mid-19th century by Francis Guthrie. Guthrie noticed that four colors were sufficient to color the map, and he wondered if this was true for every map. Many mathematicians attempted to solve the problem, but rigorous mathematical proof remained elusive. It became one of the most famous mathematical problems of the 20th century and Kenneth Appel and Wolfgang Haken finally solved computer-aided proof in 1976. This proof was considered controversial due to the extent of the computer assistance required. The 4-Colour Theorem has important applications in real-world situations, such as in scheduling and timetabling problems. It also demonstrates the power and elegance of mathematical reasoning, as well as the importance of collaboration and innovation in solving complex problems.

We describe a specific class of graphs (see Appendix A) called Standard Graphs (SG), which are constructed by the Expanded Operations e(+, pi) and e(-, pi), which are used to replace planar graphs since they may have a significant number of unsaturated links and lack uniformity. The Proof begins with "Triangulations of Euler Convex Polygons": convex polygons can be sliced into multiple triangles (Euler obtains the famous Catalan Number [2] by counting the number of triangulations of convex polygons [3]). In this article, we defined all the possible triangulations sets of convex polygons (denoted by "bound") as "All Phase States (AP)". If the boundary of any Standard Graph (SG) is All Phase States (AP) and 4-colorable, the 4-Colour Theorem will be established. Unfortunately, the All Phase States (AP) property of the boundary cannot keep Invariance during the Expanded Operation e(+, pi) (denoted by "IEO"), which implies that the All Phase States (AP) property is incomplete. Thus, the boundary of the Standard Graph must have a cryptic property that can satisfy both the All Phase States (AP) and IEO. Finally, I find that the Standard Graph's boundary satisfies 3CP and 4-colorable (denoted by "4-3CP") and it is proven 4-3CP is IEO. This article's primary goal is to attest the Standard Graph’s boundary J(m) and all its sub-bounds set {J(m’)} are 4-3CP.

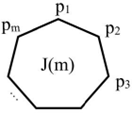
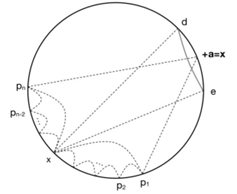
Set a cycle C(Pm, Lm), Pm = {p1, p2, ···, pm}, Lm = {p1p2, p2p3,···,pm-1pm, pmp1}, m ≧ 3, cycle C divides the plane into two connected domain: inside and outside, then we call the cycle C be a bound (see Figure 1), denoted by J(m) or J(Pm).

|J(m)| = m is the number of points of J(m), ||J(m)|| = m is the number of links of J(m). There are two types of link: real link "—" (p1-p2, p2-p3,···) and virtual link "···" (p1···p4, p3···p5, ···) although the two points aren’t linked by a real link, the virtual link is existed between them cause they are colored differently.

Figure 1: Bound

Set a bound J(m), we get points set Pm’ ⊆ Pm to form some new bounds J(m’), J1, J2, ···, (without cut links and loops), which are called sub-bounds of J(m). The J(m’), J1, J2, ··· is sub-bounds set {J(m’)} of J(m). The sub-bounds set {J1, J2, ···} is called com-bound J (m’) = J(m)-J(m’) = J1 + J2 + ··· of J(m’) in J(m).

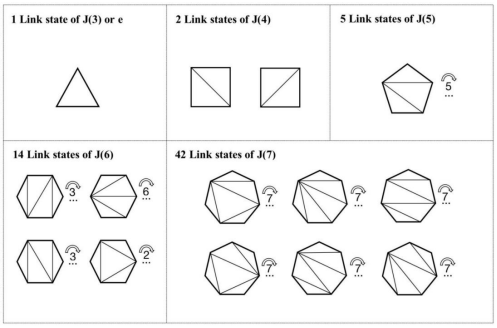
We defined a triangulation of convex polygons as a link state and provided samples of J(3)-J(7) in Table 1. If the bound J(m) contains all link states, we call J(m) all phase states (AP). The all-link states number of J(m+2) is C(m) = is Catalan Number).

Set {J(m’)} be a sub-bound set of J(m), it is simple to demonstrate that all of the sub-bounds set {J(m’)} are AP if and only if J(m) is AP. The sub-bounds set {J(m’)} is AP, which means that the sub-bound J(m’) ∈ {J(m’)} is AP and independent.

Table 1: Link states of J(3)-J(7).

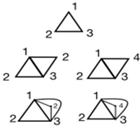
Table 2: An example of the 3-Colour All Phase States (3CP).

The 3-Colour All Phase States (3CP)

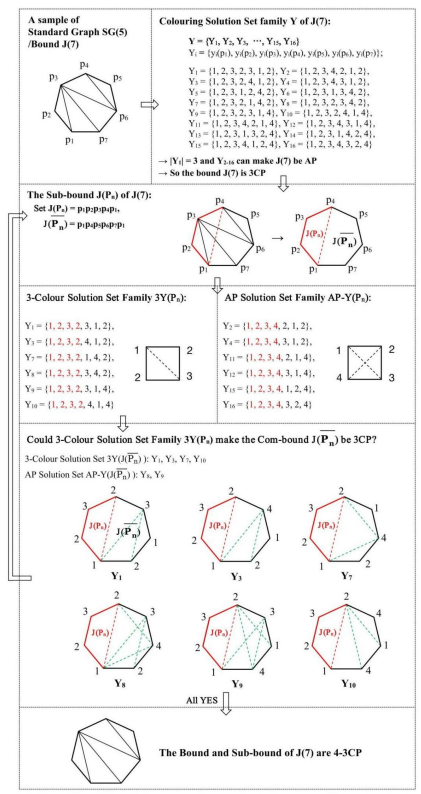
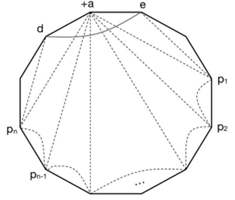
Let J(Pm) be the boundary of Standard Graph SG (see Figure 2), Y is the colouring solution set family of J(Pm), if Y can make the bound J(Pm) be AP and ∃ 3Y∈ Y, we call J(Pm) 3-Colour All Phase State (3CP). An example of 3CP is provided bellow (Table 2):

If we have enough time to test all of the Standard Graph conditions, we will discover that the boundary of every Standard Graph is 3CP and 4-colorable. It's exciting that this regularity was discovered for the first time and the 4-3CP invariance can naturally derive the 4-Colour Theorem.

Figure 2: J(Pm) of SG

The conjecture is described as follows:

4-3CP Conjecture: ∀ standard graph SG, J(m) is the boundary of SG, let Y is the coloring solution set family of J(m), {J’(m)} is sub-bounds set of J(m), Y can make:

1. |Y| ≦ 4,
2. J(m) be 3CP,
3. {J’(m)} be 3CP,
4. ∃ a 3-colour solution set 3Y(J’(m)) and { ’ (m)}be 3CP,
5. Let x, p1, p2 ∈ J’(m), link x-p1, x-p2 form sub-bounds J’1(x-p1), J’2(x-p2), and if x scans on p1→p2, ∃ 3Y(J’1+ J’2) and is 3CP.

By Exhaustive Method, it’s easy to see:

1. Element e = SG(1), J(3) conform to 4-3CP Conjecture.
2. SG(2), J(4) conform to 4-3CP Conjecture.
3. SG(3), J(3) conform to 4-3CP Conjecture.

Set a Standard Graph SG, the boundary J(Pm) of SG, the coloring solution set family Y of J(Pm), |Y|≦4, J(Pm) and it’s sub-bounds J(Pm’) conform to the 4-3CP Conjecture. Then add an element e(ade) (points a, d, e form a triangle) on the J(Pm) to form a new boundary denoted by J(a + Pm) = J(Pm) + e(ade) (d, e ∈ J(Pm), d-e, a is new). According to the Points Scanning Method (see Appendix C), it’s easy to prove J(a + Pm) is 3CP and 4-colorable, so 4-3CP Conjecture (2) is proven.

Next, we shall prove the sub-bounds set {J(a + Pm’)} of J(a + Pm) is 3CP and 4-colorable: When |Y| = 3, J(Pm) is AP equals to J(Pm) is 3CP. Since J(Pm) is AP, so the sub-bounds set {J(Pm’)} is AP, and Y(J(Pm’)) ∈ Y, |Y(J(Pm’)) | = |Y| = 3, so {J(Pm’)} is 3CP.

Then we shall prove when |Y| = 4, the sub-bounds set {J(a + Pm’)} of J(a + Pm) is 3CP.

When the new point a ∈ 3-colour sub-bound of J(a+Pm)

Take any n points Pn = {p1, p2, p3, ···, pn} ⊆ Pm, link p1-p2, p2-p3, ···, pn-1-pn, form (n-1) sub-bounds J(p1-p2), J(p2-p3), ···, J(pn-1-pn), and take any point x, x∈Pn, x ≠ p1, pn, link x with p1, pn form two sub-bounds J(x→pn) and J(p1→x); link x with d, e form J(x→pnd), J(x→ep1) and e(xde) (see Figure 3).

Figure 3: a ∈ 3-colour sub-bound of J(a + Pm), a = x.

According to J(Pm) and the sub bounds of J(Pm) are 4-3CP: J(p1-p2), J(p2-p3), ···, J(pn-1-pn) and J(x→pn), J(p1→x) and J(x→pnd), J(x→ep1), e(xde) are 3CP. According to 4-3CP Conjecture, when x scans on Pn (x ≠ p1, pn), the colouring solution set family Y(Pn) (Y(Pn) ∈ Y) must have a 3-colouring solution set 3Y(Pn) make J(p1-p2),

J(p2-p3), ···, J(pn-1-pn) and J(x→pnd), J(x→ep1), e(xde) are 3CP.

If y(a) = y(x), 3Y(Pn) will make |Y(J(a + Pn))| = 3 and make J(a→pnd), J(a→ep1) and J(p1-p2), J(p2-p3), ···, J(pn-1-pn) are 3CP, which means {J(a + Pn)} are 3CP. So, ∃ a 3-colouring solution set 3Y(J()) make {(J} be 3CP.

4-3CP Conjecture (4) is proven.

When the new point a ∉ 3-colour sub-bound of J(a + Pm)

Figure 4: a ∉ 3-colour sub-bound of J(a + Pm).

Since point a ∉ 3-colour sub-bound of J(a + Pm), we shall to prove all sub-bound J(a + Pm’) with point a are AP. Take any n + 2 points Pn = {d, e, p1, p2, p3, ···, pn} ⊆ Pm, link e-p1, p1-p2, p2-p3, ···, pn-1-pn, pn-d, form (n + 2) sub-bounds J(p1-p2), J(e-p1), J(p2-p3), ···, J(pn-1-pn), J(pn-d) and J(a + Pn). (See Figure 4)

According to the boundary J(Pm) and the sub bounds of J(Pm) are 3CP: J(Pn), J(e-p1), J(p1-p2), J(p2-p3), ···, J(pn-1-pn), J(pn-d) are 3CP, ∃ 3-colouring solution set 3Y(J(Pn)) ∈ Y, make {J(Pn)} be 3CP. According to the Points Scanning Method: If y(a) ∉ 3Y(J(Pn)) and y(a) ∈ Y, J(a + Pn) is AP, so all sub-bound J(a + Pm’) with point

a are AP.

Sum up 5.1.1, 5.1.2, we can see 4-3CP Conjecture (3) is proven.

Proof of 4-3CP Conjecture (5)

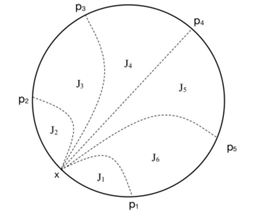
Set Pm’ ⊆ Pm, Pm’ divide J(m) into m’ parts, let x is a point between p1→p2 (x ≠ p1, p2) on J(m), we call p1, p2 are fixed points, x is scanning point. Link x-p1, x-p2, ···, x-pm’, form sub-bounds set {Ji(x) | x ∈ Ji(x), i=1, 2, ···, m’} of J(m). (Assume m’ = 5, see Figure 5).

Figure 5: sub-bounds set {Ji(x) | x ∈ Ji(x), Ji(x) ∈ J1, ···, J6} of J(m).

According to 4-3CP Conjecture (5), when x scans on p1→p2, ∃3Y(J1+ J2), and J3, ···, Jm’, Jm’+1 are 3CP. Then add a new point a on J(m), when point a is on J1, J2, ∃ y(a) ∈ Y(J1(x) + J2(x)), keep |Y(J1(x) + J2(x))| = 3, and J3, ···, Jm’, Jm’+1 are 3CP; when point a is on J3, ···, Jm’, Jm’+1, ∃ y(a) ∈ Y, keep J3, ···, Jm’, Jm’+1 are 3CP; when point a is a fixed point as p1, p2, we also could prove that, when x scans on p1→p2, ∃ 3Y(J1+ J2), and J3, ···, Jm’, Jm’+1  are 3CP (we will prove in detail in next article), so J(m + a) can keep when x scans on p1→p2, ∃ 3Y(J1+ J2), and J3, ···, Jm’, Jm’+1 are 3CP. So 4-3CP Conjecture (5) is proven.

So Y(a + m) can make:

(1) |Y(a + m)| = |Y| ≦ 4,

the bound J(a + m) be 3CP,

∀ sub-bounds set {J’(a + m)} be 3CP,

∃ a 3-colour solution set 3Y(J’(a + m)), and { J’(a+m)} be 3CP.

Let x, p1, p2 ∈ J’(a+m), link x-p1, x-p2 form sub-bounds J’1(x-p1), J’2(x-p2), J’1 + J’2, if x scans on p1→p2, ∃ 3Y(J’1+ J’2) and J’1 + J’2 is 3CP.

Above all, we have proven 4-3CP Invariance during the Expanded Operation e(+,

pi), It’s easy to see 4-3CP Invariance during the Expanded Operation e(-, pi) is also true.

So, 4-3CP Conjecture is proven!

The major research objects are the boundary’s invariance property of Standard Graph in this work. By creating the Standard Graph via Expanded Operations e(+, pi) and e(-, pi), the complexity of the planar graph is reduced. By examining the Invariance during Expanded Operations (IEO) of Standard Graph, huge calculation for coloring planar graph are avoided. Based on the above optimization method, we have demonstrated a rigorous proof of the 4-Colour Theorem, which can be also used to optimize complex systems.